f(x)
[ 1. 2. 4. 7. 11. 17.]Gradient와 수치미분
\({\bf x} =\begin{bmatrix}x_1&x_2&\dots&x_m\end{bmatrix}^T\)일 때, \(x\)에 대한 다변수함수 \(f({\bf x})\)의 gradient는 다음과 같다.
\[\begin{aligned} &\text{gradient of }f({\bf{x}}) = \frac{\partial f}{\partial {\bf x}} = \nabla f(\bf{x}) = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial }{\partial x_m} \end{pmatrix} \end{aligned}\]함수가 가지는 모든 변수에 대해서 편미분 한 뒤 모아놓은 벡터라고 생각하면 된다. 함수의 수식을 알고 미분이 가능하면 우리는 해석적으로 미분해서(미분공식써서) 그레디언트를 구하고 각각의 어떤 point에서의 편미분계수들도 구할 수 있다. 그러나 우리가 주어진 데이터는 함수f의 함숫값들이 주어진다. 예를 들면 다음과 같다.
위와 같은 함숫값들만 주어질때에는 원래의 함수를 알기는 불가능하다. 따라서 도함수를 통한 정확한 미분계수를 구하기가 불가능하므로 주어진 데이터로 \(\bf x\)에서의 미분계수의 값을 근사적으로 구할 수 있는데 이를 수치미분이라 한다.
Taylor Series
수치미분을 구하기 위해서는 먼저 테일러 급수가 나온다. 함수 \(f\)가 a를 포함하는 구간에서 무한번 미분 가능할 때, \(x = a\)에서 \(f(x)\)의 테일러 급수 전개(근사)는 다음과 같다.
\[f(x) = \sum_{n=0}^{\infty}\frac{f^{n}(a)}{n!}(x-a)^n = f(a) + \frac{f^{'}(a)}{1!}(x-a) + \frac{f^{''}(a)}{2!}(x-a)^2 + \dots \] 테일러급수는 어떤 함수를 다항함수의 합으로 표현하며 한점a에서의 미분계수의 합으로 표현한다는 것에 의미가 있다. 다만 주의할 점은 \(a\)의 위치와 다항식의 차수이다. \(a\)가 \(x\)근처에 가까울 수록 원래의 함수를 잘 근사하며 다항식의 차수 \(n\)이 클수록 오차가 작아진다.
수치미분
위에서 언급했듯이 수치미분은 주어진 데이터를 가지고 어떤 지점에서의 미분계수의 \(\bf x\)에서의 미분계수의 값을 근사적으로구하는 것이다. 각각의 방법으로 \(x_j\)에서의 미분계수(기울기)의 근삿값을 구해보면 다음과 아래의 그림과 같다. 가장오른쪽에 중앙차분법(central divided difference approximation)에 의한 기울기가 실제기울기와 가장 비슷해보인다.
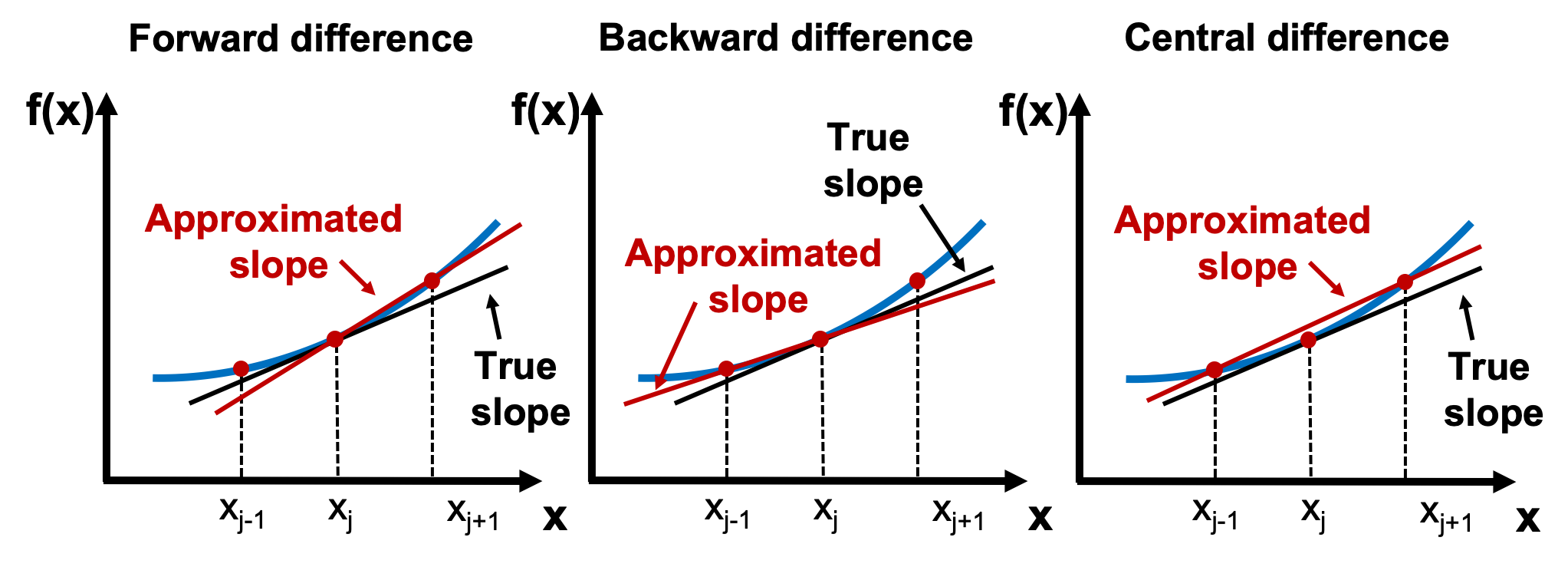
유한차분법의 각각의 방법으로 도함수의 근사값을 유도하면 다음과 같다. (유도 : Section 5)
전향차분근사 \[\begin{align} &f'(x_i) \overset{\sim}{=} \frac{f(x_{i+1})-f(x_i)}{h}\\ &O(h) = - \frac{hf^{''}(x_i)}{2!} - \frac{h^2f^{'''}(x_i)}{3!} - \dots\\ &\text{where, } h = x_{i+1} - x_i \nonumber \end{align}\]
여기서 \(O(h)\)는 무한한항을 유한한항으로 근사시킬때 나타나는 절단오차라고 하며 h가 포함된 항이 가장 크게 기여하므로 \(O(h)\)로 표기한다. 절단오차에서 h의 차수는 크면 클수록 좋다. \(p<q\)라 가정하고 같은 구간안에서 더 많은 데이터를 얻었다고 하면 \(h\)가 작아지면 작아질수록 \(h^p\)가 최고차항인 절단오차 \(O(h^p)\) 보다는 \(h^q\)가 최고차항인 \(O(h^q)\)가 더 빨리 작아지기 때문이다.
(1)번식을 도함수\(f'(x_i)\)의 (1차)전향차분근사라고 한다.\(x_i\)의 도함수(미분계수)를 구하기 위해 \(x_{i+1}\)을 사용했기에 전향 + 절단오차의 차수가 1인 \(O(h)\)이기 떄문에 그렇다.
후향차분근사 \[\begin{align} &f'(x_i) \overset{\sim}{=} \frac{f(x_{i})-f(x_{i-1})}{h}\\ &O(h) = \frac{h}{2!}f^{''}(x_i) - \frac{h^2}{3!}f{'''}(x_i)+\dots \\ &\text{where, } h = x_{i} - x_{i-1}, \nonumber \end{align}\]
(1)번식을 도함수\(f'(x_i)\)의 (1차)후향차분근사라고 한다.\(x_i\)의 도함수(미분계수)를 구하기 위해 \(x_{i-1}\)을 사용했기에 후향 + 절단오차의 차수가 1인 \(O(h)\)이기 때문이다. 또한 후향차분근사의 절단오차는 전향차분근사와 마찬가지로 \(O(h)\)로 서로 동일하다.
중앙차분근사
\[\begin{align}
&f'(x_i) \overset{\sim}{=} \frac{f(x_{i+1})-f(x_{i-1})}{2h}\\
&O(h) = - \frac{h^2}{3!}f{'''}(x_i)+\dots \\
&\text{where, } h = x_{i} - x_{i-1} = x_{i+1} - x_i\nonumber
\end{align}\]
(1)번식을 도함수\(f'(x_i)\)의 (2차)중앙차분근사라고 한다.\(x_i\)의 도함수(미분계수)를 구하기 위해 \(x_{i-1},x_{i+1}\)을 사용했기에 중앙이라는 단어가 붙었고 절단오차의 차수가 2인 \(O(h^2)\)이기 때문이다. 또한 (2차)중앙차분근사의 절단오차는 \(O(h^2)\)으로 최고차항이 \(h\)인 전향,후향차분근사와는 다르다. 이는 같은 데이터를 가졌다고 하더라도 중앙차분근사법으로 구한 도함수의 근삿값이 해석적으로 구한값과 가장 비슷하며 또한 같은구간에서 데이터를 더 많이 취득할수록 더 빠르게 정확한값가 가까워짐을 의미한다.
np.gradient?
넘파이의 그레디언트 함수는 배열의 끝값을 제외한 내부의 포인트에서는 2차중앙차분근사(second order accurate central differences)를 미분계수를 계산하고 가장끝값에 있는 포인트들에대해서는 1차 혹은 2차 one-side 차분(전향,후향차분)근사를 통해서 수치미분을 해주는 함수다.
1차원 배열의 경우
Ex) \(dx\) = 1
넘파이 1차원 배열이 다음과 같이 주어져 있다고 하자.
[ 1. 2. 4. 7. 11. 16.]np.gradient함수는 1차원 배열의 내부에 있는 각각의 값들은 \(x\)값이 거리가 \(dx\)=1씩 변화할때마다의 함숫값\(f(x)\)들로 이해한다. 즉,다음과 같다.
\(x_1\)에서의 함숫값 \(f(x_1)\) = 1.0
\(x_2\)에서의 함숫값 \(f(x_2)\) = 2.0
\(x_3\)에서의 함숫값 \(f(x_3)\) = 4.0
\(x_4\)에서의 함숫값 \(f(x_4)\) = 7.0
\(x_5\)에서의 함숫값 \(f(x_5)\) = 11.0
\(x_6\)에서의 함숫값 \(f(x_6)\) = 16.0
\[\begin{aligned} &f^{'}(x_2) \overset{\sim}{=} \frac{f(x_3)-f(x_1)}{2h} = \frac{4-1}{2} = 1.5 \\ &f^{'}(x_5) \overset{\sim}{=} \frac{f(x_6)-f(x_4)}{2h} = \frac{16-7}{2} = 4.5 \\ &\text{where, } h = x_3-x_2 = x_2-x_1 = 1 \end{aligned}\] 1차원 배열의 가장 처음에 오는 값에 전향차분근사를 사용하고 가장 마지막에 오는 값에서는 후향차분근사를 사용한다. \[\begin{aligned} &f^{'}(x_1) = \frac{f(x_2) - f(x_1)}{h} = \frac{2-1}{1} = 1 \\ &f^{'}(x_6) = \frac{f(x_6) - f(x_5)}{h} = \frac{16-11}{1} = 5 \end{aligned}\]
계산한 값과 실제로 일치하는지 확인.
num_diff = np.gradient(f)
print("np.gradient의 출력값")
print(num_diff)
for i in range(len(num_diff)):
display(Markdown(rf'$x_{i+1}$에서의 도함수의 근삿값 $\frac{{dy}}{{dx}}|_{{x = x_{i+1}}}$ ~= {num_diff[i]}'))np.gradient의 출력값
[1. 1.5 2.5 3.5 4.5 5. ]\(x_1\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_1}\) ~= 1.0
\(x_2\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_2}\) ~= 1.5
\(x_3\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_3}\) ~= 2.5
\(x_4\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_4}\) ~= 3.5
\(x_5\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_5}\) ~= 4.5
\(x_6\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_6}\) ~= 5.0
Ex) \(dx \not = 1\) (default가 아닐 경우)
거리\(dx=2\)일때 계산한,\(x_2,x_5\)에서 미분계수의 2차중앙차분근사는 다음과 같다.\[\begin{aligned} &f^{'}(x_2) \overset{\sim}{=} \frac{f(x_3)-f(x_1)}{2h} = \frac{4-1}{4} = 0.75 \\ &f^{'}(x_5) \overset{\sim}{=} \frac{f(x_6)-f(x_4)}{2h} = \frac{16-7}{4} = 2.25 \\ &\text{where, } h = x_3-x_1 = x_6-x_4 = 2 \end{aligned}\] 거리가 \(dx=2\)일때 배열의 양 끝값에서 전향,후향차분근사를 통한 미분계수의 값은 다음과 같다. \[\begin{aligned} &f^{'}(x_1) = \frac{f(x_2) - f(x_1)}{h} = \frac{2-1}{2} = 0.5 \\ &f^{'}(x_6) = \frac{f(x_6) - f(x_5)}{h} = \frac{16-11}{2} = 2.5 \end{aligned}\]
x값 사이의 거리\(dx\)를 바꾸고 싶다면? => 두번째 인수에 스칼라 대입하면 된다.
dx = 2
num_diff = np.gradient(f,dx)
print("np.gradient의 출력값")
print(num_diff)
for i in range(len(num_diff)):
display(Markdown(rf'$x_{i+1}$에서의 도함수의 근삿값 $\frac{{dy}}{{dx}}|_{{x = x_{i+1}}}$ ~= {num_diff[i]}'))np.gradient의 출력값
[0.5 0.75 1.25 1.75 2.25 2.5 ]\(x_1\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_1}\) ~= 0.5
\(x_2\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_2}\) ~= 0.75
\(x_3\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_3}\) ~= 1.25
\(x_4\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_4}\) ~= 1.75
\(x_5\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_5}\) ~= 2.25
\(x_6\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_6}\) ~= 2.5
Ex) x값의 좌표를 직접 정해주는 경우
이전에는 각각의 인덱스간의 거리는 모두 동일하게 기본값 1이거나 다른값을 사용했다. 그러지 않고 \(x_1,x_2,\dots,x_6\)의 좌표를 직접 지정해주는 것도 가능하다. 함수의 2번재 인수에 좌표를 직접 넣어주면 된다.
먼저 x값의 좌표를 다음과 같다고 해보자.
x = np.array([0., 1., 1.5, 3.5, 4., 6.], dtype=float)
f = np.array([1,2,4,7,11,16],dtype=float)
print("각각의 좌표와 함숫값")
for i in range(len(x)):
display(Markdown(rf'$x_{i+1}$ = {x[i]}, $f(x_{i+1})$ = {f[i]}'))각각의 좌표와 함숫값\(x_1\) = 0.0, \(f(x_1)\) = 1.0
\(x_2\) = 1.0, \(f(x_2)\) = 2.0
\(x_3\) = 1.5, \(f(x_3)\) = 4.0
\(x_4\) = 3.5, \(f(x_4)\) = 7.0
\(x_5\) = 4.0, \(f(x_5)\) = 11.0
\(x_6\) = 6.0, \(f(x_6)\) = 16.0
각각의 좌표에서 도함수의 근삿값을 구하면 아래와 같다.(수식 계산은 잘 모르겠네요 … 추후에 더 공부하겠습니다!)
num_diff = np.gradient(f,x)
print("np.gradient의 출력값")
print(num_diff)
for i in range(len(num_diff)):
display(Markdown(rf'$x_{i+1}$에서의 도함수의 근삿값 $\frac{{dy}}{{dx}}|_{{x = x_{i+1}}}$ ~= {num_diff[i]}'))np.gradient의 출력값
[1. 3. 3.5 6.7 6.9 2.5]\(x_1\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_1}\) ~= 1.0
\(x_2\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_2}\) ~= 2.9999999999999996
\(x_3\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_3}\) ~= 3.5
\(x_4\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_4}\) ~= 6.700000000000001
\(x_5\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_5}\) ~= 6.899999999999999
\(x_6\)에서의 도함수의 근삿값 \(\frac{dy}{dx}|_{x = x_6}\) ~= 2.5
2차원 배열의 경우
2차원 배열의 경우 axis=0(세로축)과 axis=1(가로축) 두 축방향으로 계산한 도함수의 근삿값을 반환한다.axis=0일 경우 각각의 열마다 따로따로 독립적으로 \(x_1,x_2...\)에 대한 함숫값\(f(x_1),f(x_2),\dots\)이 있다고 생각하면 되고 axis=1일 경우 각각의 행마다 따로따로 독립적으로 \(x_1,x_2...\)에 대한 함숫값\(f(x_1),f(x_2),\dots\)이 있다고 생각하면 된다.또한 1차원 배열과 유사하게 각각의 행,열의 끝값에는 전향or후향차분근사를 행,열의 내부에 있는 값은 중앙차분근사를 사용한다.
Ex) \(dx=1,dy=1\)
2차원 배열은 다음과 같다.
Ex) \(dx \not = 1,dy \not = 1\) (default가 아닌 경우)
각각의 행,열마다 거리를 따로 설정해주고 싶은 경우? => 스칼라 2개 인수로 전달.
dx = 2;dy = 2
ax0_difcoef,ax1_difcoef= np.gradient(np.array([[1, 2, 6], [3, 4, 5]], dtype=float),dx,dy)
print(f'axis = 0 방향으로 도함수의 근삿값 계산 \n{ax0_difcoef}')
print(f'axis = 1 방향으로 도함수의 근삿값 계산 \n{ax1_difcoef}')axis = 0 방향으로 도함수의 근삿값 계산
[[ 1. 1. -0.5]
[ 1. 1. -0.5]]
axis = 1 방향으로 도함수의 근삿값 계산
[[0.5 1.25 2. ]
[0.5 0.5 0.5 ]]Appendix
전향차분근사 유도
\(x_1,x_2,\dots,x_{i-1},x_i,x_{i+1},\dots,x_n\)과 각각에 대응하는 함숫값 \(f(x_1),f(x_2),\dots,f(x_{i-1}),f(x_i),f(x_{i+1}),\dots,f(x_n)\) 주어진 데이터라고 가정하자. 목적은 x_i에서의 미분계수를 구하는 것이다. \(a = x_i\)에서 함수\(f(x)\)의 테일러 급수 근사는 다음과 같다.
\[f(x) = \sum_{n=0}^{\infty}\frac{f^{n}(x_i)}{n!}(x-x_i)^n = f(x_i) + \frac{f^{'}(x_i)}{1!}(x-x_i) + \frac{f^{''}(x_i)}{2!}(x-x_i)^2 + \dots \]
\(x=x_{i+1}\)에서의 함숫값은 다음과 같다.
\[f(x_{i+1}) = \sum_{n=0}^{\infty}\frac{f^{n}(x_i)}{n!}(x_{i+1}-x_i)^n = f(x_i) + \frac{f^{'}(x_i)}{1!}(x_{i+1}-x_i) + \frac{f^{''}(x_i)}{2!}(x_{i+1}-x_i)^2 + \dots \]
\(f'(x_i)\)가 포함된항만 남겨두고 나머지는 이항하면 다음과 같다.
\[f^{'}(x_i)(x_{i+1}-x_i) = f(x_{i+1}) - f(x_i) - \frac{f^{''}(x_i)}{2!}(x_{i+1}-x_i)^2 + \dots\]
\(h = x_{i+1}-x_i\)로 두고 양변을 h로 나누면 다음과 같다.
\[f'(x_i) = \frac{f(x_{i+1})}{h} - \frac{f(x_i)}{h} - \frac{hf^{''}(x_i)}{2!} - \frac{h^2f^{'''}(x_i)}{3!}\]
여기서 우변의 두개의 항만 남겨두고 \(O(h) = - \frac{hf^{''}(x_i)}{2!} - \frac{h^2f^{'''}(x_i)}{3!} - \dots\)라 하면 다음과 같다.
\[\begin{align}
&f'(x_i) \overset{\sim}{=} \frac{f(x_{i+1})-f(x_i)}{h}\\
&O(h) = - \frac{hf^{''}(x_i)}{2!} - \frac{h^2f^{'''}(x_i)}{3!} - \dots\\
&\text{where, } h = x_{i+1} - x_i \nonumber
\end{align}\]
후향차분근사 유도
\(x_1,x_2,\dots,x_{i-1},x_i,x_{i+1},\dots,x_n\)과 각각에 대응하는 함숫값 \(f(x_1),f(x_2),\dots,f(x_{i-1}),f(x_i),f(x_{i+1}),\dots,f(x_n)\) 주어진 데이터라고 가정하자. 목적은 x_i에서의 미분계수를 구하는 것이다. \(a = x_i\)에서 함수\(f(x)\)의 테일러 급수 근사는 다음과 같다.
\[f(x) = \sum_{n=0}^{\infty}\frac{f^{n}(x_i)}{n!}(x-x_i)^n = f(x_i) + \frac{f^{'}(x_i)}{1!}(x-x_i) + \frac{f^{''}(x_i)}{2!}(x-x_i)^2 + \dots \]
\(f(x_i)\)는 다음과 같다.
\[f(x_{i-1}) = \sum_{n=0}^{\infty}\frac{f^n(x_i)}{n!}(x_{i-1}-x_i)^n = f(x_i) + \frac{f^{'}(x_i)}{1!}(x_{i-1}-x_i) + \frac{f^{''}(x_i)}{2!}(x_{i-1}-x_i)^2+\dots \]
1차미분이 포함된 항만 남기고 나머지는 이항하면 다음과 같다.
\[f^{'}(x_i)(x_{i-1}-x_i) = f(x_{i-1}) - f(x_i) - \frac{f^{''}(x_i)}{2!}(x_{i-1}-x_i)^2-\frac{f^{'''}(x_i)}{3!}(x_{i-1}-x_i)^3-\dots \]
\(h = x_{i} - x_{i-1}\)로 놓으면 다음과 같다.
\[f^{'}(x_i)(-h) = f(x_{i-1}) - f(x_i) - \frac{f^{''}(x_i)}{2!}h^2+\frac{f^{'''}(x_i)}{3!}h^3-\dots \]
\[\begin{aligned} f^{'}(x_i) &= \frac{f(x_{i-1})}{-h} + \frac{f(x_i)}{h} + \frac{f^{''}(x_i)}{2!}h-\frac{f^{'''}(x_i)}{3!}h^2+\dots \\ &=\frac{f(x_i)-f(x_{i-1}) }{h} + \frac{f^{''}(x_i)}{2!}h-\frac{f^{'''}(x_i)}{3!}h^2+\dots \end{aligned}\]
마찬가지로 우변의 두개 항만 남겨두고 \(O(h) = \frac{hf^{''}(x_i)}{2!} - \frac{h^2f^{'''}(x_i)}{3!} + \dots\)라 하면 다음과 같다. \[\begin{align} &f'(x_i) \overset{\sim}{=} \frac{f(x_{i})-f(x_{i-1})}{h}\\ &O(h) = \frac{h}{2!}f^{''}(x_i) - \frac{h^2}{3!}f{'''}(x_i)+\dots \\ &\text{where, } h = x_{i} - x_{i-1}, \nonumber \end{align}\]
중앙차분근사 유도
전향차분근사와 후향차분근사의 유도과정에서의 테일러 전개식은 다음과 같다.
\[f'(x_i) = \frac{f(x_{i+1})}{h} - \frac{f(x_i)}{h} - \frac{hf^{''}(x_i)}{2!} - \frac{h^2f^{'''}(x_i)}{3!} - ...\] \[f'(x_i) = \frac{f(x_{i})}{h} - \frac{f(x_{i-1})}{h} + \frac{hf^{''}(x_i)}{2!} - \frac{h^2f^{'''}(x_i)}{3!} + ...\]
마찬가지로 우변의 두개 항만 남겨두고 절단오차\(O(h^2) = -\frac{h^2f^{'''}(x_i)}{3!} - \dots\)라 하면 다음과 같다. \[\begin{align} &f'(x_i) \overset{\sim}{=} \frac{f(x_{i+1})-f(x_{i-1})}{2h}\\ &O(h) = - \frac{h^2}{3!}f{'''}(x_i)+\dots \\ &\text{where, } h = x_{i} - x_{i-1}\,\,\text{or}\,\, h = x_{i+1} - x_i\nonumber \end{align}\]